Fast, Hacky Geospatial Queries with UTFGrid
- UTFGrid is no longer supported or developed.
- This tile-based strategy is now the core strategy of Carmen, the technology behind Mapbox's geocoding service. It uses vector tiles, though, instead of raster-like grids.
- see this map in full-screen </span>
People in Places
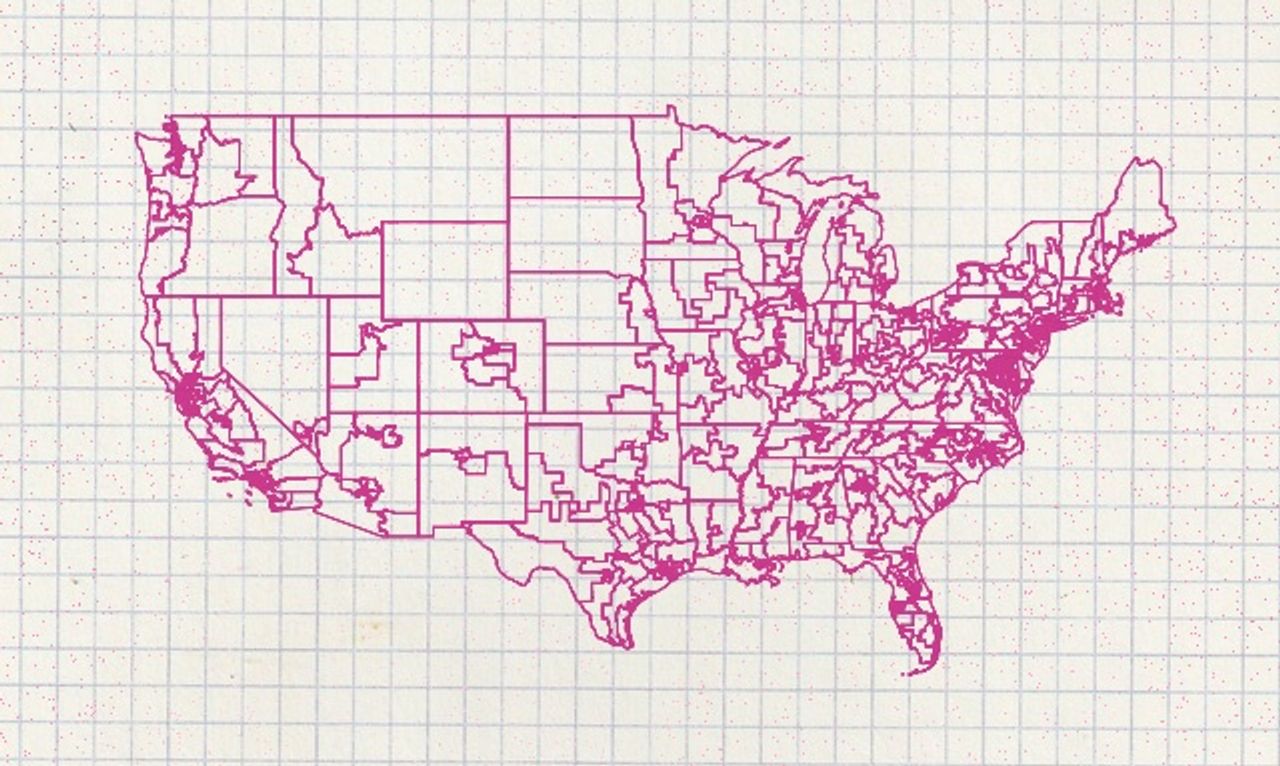
How do you know what congressional district you’re in? Or state, town, census block, etc? It’s the Point in Polygon problem, which has a bunch of really cool strategies like ray casting - but without doing some real indexing, it’s not easy to do this kind of problem fast with a ton of polygons. SimpleGeo does this to the max: their context service does crazy-fast lookups of all of the various stuff about your place.
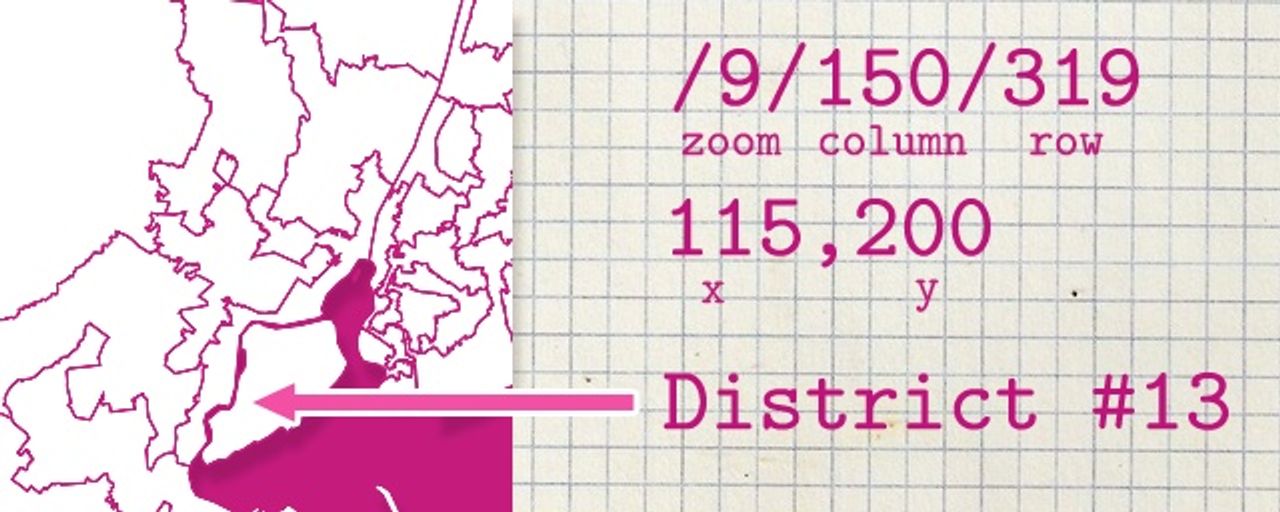
However, if you cheat a little, it’s possible to do it in constant time, and with very little technology or server power - so searching for a point in a million polygons is very fast. The trick is rasterized, precomputed data, and there’s a pretty quick example of this: the UTFGrid spec that we use for map interactivity
is rasterized data: it’s like pixels of data. And instead of a complex indexing scheme, we’ve just got simple XYZ tiles at every zoom level, and it’s straightforward to find a tile URL for a given latitude longitude point.
Essentially it’s like having a hash table of all of the pixel locations in the world: from a latitude/longitude point, you can figure out an address and pull it out without doing any hard thinking.
So usually we get this magical data through Wax
and wrap it up in a lot of fancy code so that you see tooltips and other stuff when you hover over points. The actual code related to managing grids, though, doesn’t care about a map or a mapping framework. And for finding tiles, I use node-sphericalmercator, which, despite the name, works great in-browser. After filling its cache, you can get px values for latitude longitude in constant time.
A quick demo! Your friendly 110th congressional districts (which are easy to grab from census.gov and were not changed for the 111th congress ): aren’t the most grueling test, with 436 shapes, but are kind of cool, because if you’re in the US, you’re in one. Sorry, international readers.
So! Just code up a quick bit of code I’ll call utfgridquery, that wires together little parts of Wax without any maps, and you have this:
Try it Out
protip: if you’ve got a modern browser, you can leave the address field blank and it’ll find you automatically. if it asks permission to share your location, do so - it’s not stored or shared.
Limitations
This current approach takes much of its speed from the fact that the data is precomputed. Fast rendering in Mapnik makes this possible, and in the future we’ll be doing live rendering, but for the time being it’s cool that TileStream or even static tiles can power this search.
Next up: resolution. We’re dealing with pixels, here, not platonic solids. Luckily it’s fairly easy to do the math. (hat tip to multiplans’s concise explanation ). Since we’re doing 4px resolution grids, even a 256×256px tile isn’t full resolution. What we get out of the equation is how many meters are in a pixel: the maximum error of the match.
Why? Because a tile is 256 pixels wide, and the world is 2^(z-1) tiles wide and high at each zoom level z. The world is 6378137 meters from its centerpoint to the surface, so r is that for this purpose. (not really)
Note that zoom levels start with 0, and we’re doing 2^(z-1), so at zoom level 0, it’s 2^-1 = 0.5, so the radius of the world, gets multiplied by 2pi - giving the circumference. And, finally, multiply by 0.25 to reduce the resolution because we’re actually just storing one ‘pixel’ for each 4px block of an image.
What’s Next
There’s more to do here: in the next episode, I’ll show that it’s possible to translate another problem - finding the nearest point - to this same problem space, and then be able to solve it in the same perfectly constant time as we do here. But the basics are: using tiled UTFGrid lets us do point-in-polygon tests in contant time, thanks to rasterization and pre-rendering. It’s pretty easy to pull off, code-wise, doesn’t require a server component, and could be pretty neat for groups like voter registration campaigns or location-based services with some need for context. Basically, for finding things within things, this is a pretty cool hack.
- not really: The earth’s radius is actually really variable, as you’ll find in this nice article. It’s not a ball, and isn’t a regular ellipsoid either, though it can pass for either if you’re willing to fudge the numbers.